21 谱线的形成#

就像人和人之间有样貌差异一样，恒星的样貌——光谱——也是各自不同的。在这些各种各样的恒星光谱中，我们可以通过提取它们之间一致的特征以及稍有不同的性质来进行分类。本节我们在定性理解光谱吸收线和表面温度之间的关系的同时，用简单的模型进行定量的计算。

21.1 光谱谱线的消长#

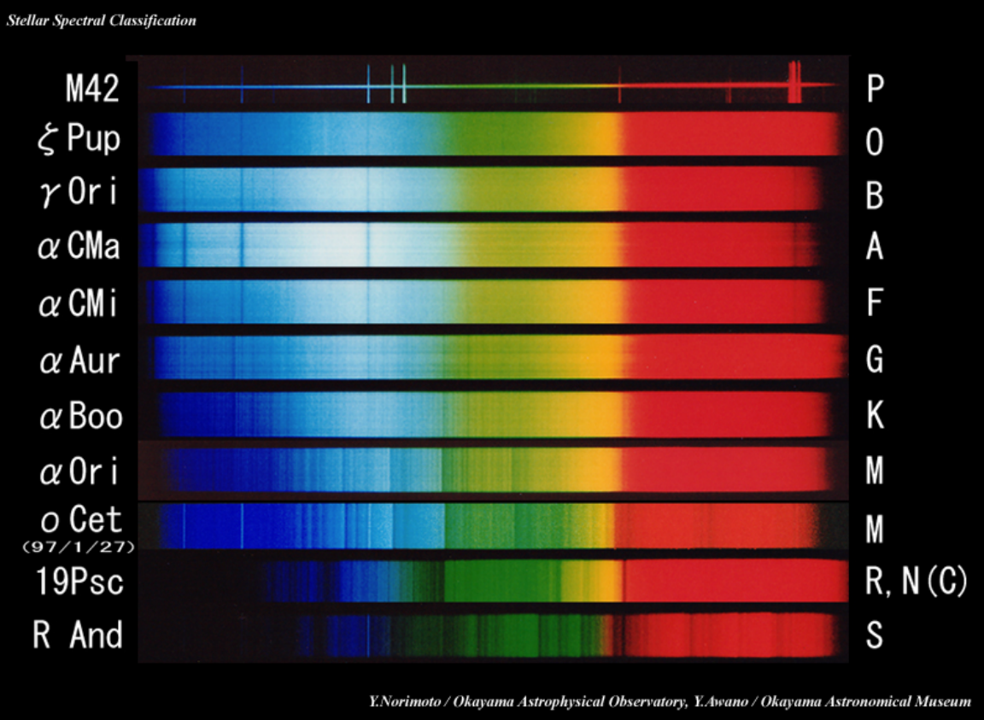
回顾一下前一节的图20.3（上图）以及表20.1，我们会发现光谱谱线（特别是吸收线）的强度随着光谱型的不同有很大的变化。以氢原子(HI)线的巴尔末线为例，O型星的线强度较弱，A型星的强度最强，F型以及之后的线强度又变弱了。氦原子(HeI)谱线最强的是温度稍微高一点的B型星。而被称为H和K线的电离钙(CaII)线在高温恒星中很弱，但是在F型和G型星的光谱中很强。图21.1画出了一些吸收线强度随光谱型的变化。

图21.1

图21.1 H (HI)、HeI、FeI、CaII等吸收线强度的变化

这样的谱线消长虽然和元素的量以及大气密度是有关系的，但是最大的原因是恒星大气的温度（比A型星温度要低的恒星虽然没有氦的吸收线，但这并不意味着低温恒星中就没有氦元素了）。

定性地说，我们可以这样考虑。以氢的巴尔末吸收线为例；氢的巴尔末线是氢原子被激发到第1激发态之后，再吸收光子并被激发到更高的激发态所形成的吸收线（第9节）。所以说，处于第1激发态的氢原子越多、巴尔末线就会越强。对于表面温度较低的M型、K型等恒星来说，氢原子基本上都处于基态，巴尔末线就比较弱。 G型到F型的恒星温度较高，有部分氢原子处于第1激发态，所以巴尔末线变强。但是随着恒星的表面温度继续升高，氢原子逐渐电离，导致中性氢原子占比下降，巴尔末线又逐渐变弱。

像这样的原子激发和电离的温度根据元素种类以及态的不同是不一样的，所以形成了像图21.1的曲线分布。反过来说，在知道了可见光波段许多不同元素的吸收线强度之后，我们就可以推出这颗恒星的大气温度（光谱型）了。这就是恒星光谱分类的本质（当然实际上还要考虑其他的因素）。

下面我们定量地分析上面定性的内容。

问21.1 说明中性氦(He I)原子的吸收线在温度更高的星中更强的理由
问21.2 说明钙离子(Ca II)的吸收线在温度更低的星中更强的理由

21.2 玻尔兹曼方程#

恒星内部的气体和辐射会发生非常频繁的相互作用，处于局部热动平衡(local thermodynamic equilibrium; LTE)状态（第8节）。我们可以将统计力学的结论应用到这种热动平衡的状态中，也就意味着粒子的分布遵从玻尔兹曼方程(Boltzmann equation)。所以，处于基态的原子和处于第$i$激发态原子的数目比为：

$$ \frac{N_i}{N_0} = \frac{g_i}{g_0} e^{-\frac{\varepsilon_i}{kT}} \tag{21.1}$$

其中$g_0$和$g_i$是基态和第$i$个激发态的多重态数，$\varepsilon_i$是从基态到第$i$个激发态的能量差，$k$是玻尔兹曼常数，$T$是温度。玻尔兹曼方程描述的是处于高激发态的粒子数是随着能量的增加而指数下降的。

问21.3 温度升高时$\frac{N_i}{N_0}$如何变化？
问21.4 假设$g_i=g_0=1$，$kT=1,\mathrm{eV}$与$kT=10,\mathrm{eV}$，写出$\frac{N_i}{N_0}$的表达式.

21.3 萨哈方程#

气体温度非常高时，有一部分原子会被电离：原子失去一个电子，而失去的这个电子成为自由电子。虽然中性态和电离态的平衡也是热平衡的一种，但是一般会把这种平衡状态成为电离平衡。电离平衡的表达式称为萨哈方程。处于中性态的原子数$N_\mathrm{I}$和处于1次电离态的原子数$N_\mathrm{II}$的比为：

$$ \frac{N_\mathrm{II}}{N_\mathrm{I}} = \frac{2 u_\mathrm{II}}{u_\mathrm{I}} \frac{(2\pi m_\mathrm{e} kT)^{3/2} }{h^3 N_\mathrm{e}} e^{-\frac{\chi}{kT}} = \frac{2 u_\mathrm{II}}{u_\mathrm{I}} \frac{(2\pi m_\mathrm{e})^{3/2} (kT)^{5/2}}{h^3 P_\mathrm{e}} e^{-\frac{\chi}{kT}} \tag{21.2}$$

其中$u_\mathrm{I}$, $u_\mathrm{II}$为配分函数，$m_\mathrm{e}$为电子质量，$h$为普朗克函数，$N_\mathrm{e}$为电子数密度($\mathrm{个~cm^{-3}}$)，$P_\mathrm{e}=N_\mathrm{e} kT$为电子压强($\mathrm{dyn cm^{-2}}$)，$\chi$是电离能。萨哈方程说明了电离能越高的电离态粒子数越少。

问21.5 温度升高时$\frac{N_\mathrm{II}}{N_\mathrm{I}}$如何变化？
问21.6 假定配分函数为1，用以下条件计算$\frac{N_\mathrm{II}}{N_\mathrm{I}}$的值。 1）G型星($T=6000,\mathrm{K}, \log{P_\mathrm{e}}=1.08$)；
2）A型星($T=10000,\mathrm{K}, \log{P_\mathrm{e}}=2.50$)；
3）B型星($T=15000,\mathrm{K}, \log{P_\mathrm{e}}=2.76$).

21.4 练习#

当我们将多重态数等参数代入并计算式$(21.1)$和$(21.2)$的话，我们可以得到与图21.1相似的吸收线强度变化图。但是考虑全部的激发态和电离态会让计算变得十分复杂，这里用下图所示的简单原子模型来计算吸收线的强度变化。

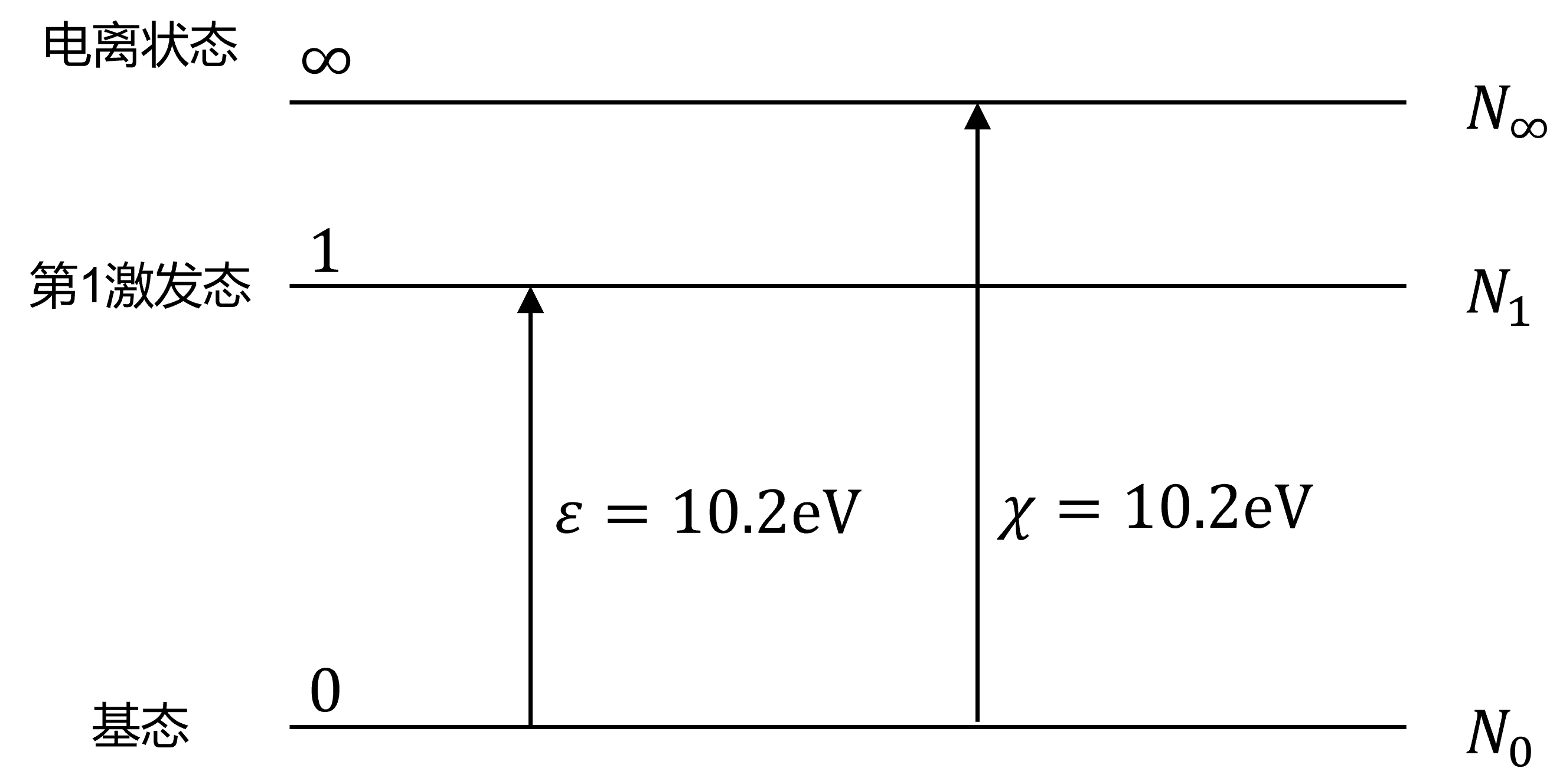图21.2 图21.2 二能级氢原子模型

这里我们将氢原子模型简化为了只有基态、第1激发态和电离态的模型原子（图21.2）。虽然我们忽略了第2激发态以及以上的的激发态，我们得到的结果仍然能近似于实际情况。令在某温度下的能级占据数为$N_0$, $N_1$和$N_\infty$（总原子数$N=N_0+N_1+N_\infty$是一个常数）。氢原子第1激发态的激发能为$10.2,\mathrm{eV}$，电离能为$13.6,\mathrm{eV}$. 根据以下顺序求$N_1/N$随温度的变化。

(1) 氢原子基态的多重态数为2，第1激发态的多重态数为8；证明此时玻尔兹曼方程变为：

$$ \frac{N_i}{N_0} = 4 e^{-\frac{\varepsilon_i}{kT}} \tag{21.3}$$

(2) 氢原子基态与电离态的配分函数比为$1/2$。证明此时萨哈方程为：

$$ \frac{N_\infty}{N_0+N_1} = \frac{(2\pi m_\mathrm{e})^{3/2} (kT)^{5/2}}{h^3 P_\mathrm{e}} e^{-\frac{\chi}{kT}} \tag{21.4}$$

恒星大气一般的电子压强$P_\mathrm{e} = 100,\mathrm{dyn~cm^{-2}}$；将它和其他式子代入式$(21.4)$，证明在cgs单位制下其为：

$$ \frac{N_\infty}{N_0+N_1} = 4.84\times10^7 (kT)^{5/2} e^{-\frac{\chi}{kT}} \tag{21.5}$$

(3) 利用式$(21.3)$求$N_1/(N_0+N_1)$在不同温度下的值，并画出它与温度的关系曲线。

(4) 利用式$(21.5)$求$(N_0+N_1)/(N_0+N_1+N_\infty)$在不同温度下的值，并画出它与温度的关系曲线。

(5) 证明

$$ \frac{N_1}{(N_0+N_1+N_\infty)} = \frac{4}{4+e^{\varepsilon/kT}} \frac{e^{\chi/kT}}{4.84\times 10^7 (kT)^{5/2} + e^{\chi/kT}} \tag{21.6}$$

画出它与温度的关系曲线并与图21.1进行比较。

注：

上面的计算结果应放入下表中：

$T [\mathrm{K}]$	$kT [\mathrm{eV}]$	$\frac{\varepsilon}{kT}$	$\frac{N_1}{N_0+N_1}$	$\frac{\chi}{kT}$	$4.84\times 10^7 (kT)^{5/2}$	$\frac{N_0+N_1}{N}$	$\frac{N_1}{N}$
5000
6000
7000
8000
9000
10000
11000
12000
13000
14000
15000

$k=1.3807\times 10^{-23},\mathrm{J~K^{-1}}$
$1,\mathrm{eV} = 1.6022\times 10^{-19},\mathrm{J}$
温度从$5000,\mathrm{K}$到$15000,\mathrm{K}$，每$500,\mathrm{K}$一个点
$(N_0+N_1)/N$和$(N_1)/N$的纵坐标分别扩大1000倍和10万倍

21.5 课后练习#

对氦原子进行和上面同样的计算。
(1) 中性氦(He I)：激发能为$20.87,\mathrm{eV}$，电离能为$24.59,\mathrm{eV}$；所有的多重态数设为1；
(2) 1次电离氦(He II)：激发能为$48.16,\mathrm{eV}$，电离能为$54.42,\mathrm{eV}$.

21 谱线的形成

Contents