第十四章:半径与有效温度的确定#
这俩参数是恒星的基本参数。假设有俩以某恒星为中心的同心球,一个半径为恒星半径$$ R
$$ 4\pi d^2 F_\nu = 4\pi R^2 \mathscr{F}_\nu \tag{14.1} $$
将有效温度的定义$$ (1.2) $$代入并积分,有
$$ \int_0^\infty F_\nu d\nu = (R/d)^2 \int_0^\infty \mathscr{F}\nu d\nu = \theta\mathrm{R}^2 \sigma T_\mathrm{eff}^4 \tag{14.2} $$
$$ \theta_\mathrm{R}
不同波段是有不同的半径的,毕竟光深和几何深度的关系随着频率而变化。同时有效温度实际上在恒星不同的表面上是不一样的(有米粒组织等),而且决定恒星大气更根本的参数是温度随着光深的分布。但是这一章我们先忽略这些东西,就看这两个参数。
半径测量#
半径测量分为直接和间接的方法。
直接方法#
干涉法#
干涉法好说,测量一个方波傅立叶变换之后的零点位置可以得出这个方波的大小,而干涉仪可以测出这个零点。现在(2003年)的精度已经达到了0.05毫角秒,有几百颗星的角直径被测出来了。
月掩星法#
也好说,测量恒星被掩食的时候的光变然后建模拟合就行。局限在于不同波度的光变幅度不一样,所以需要用比较窄的滤光片;类似的,月球边缘的起伏也会造成不同次掩食时光变和时标的不一样。当然最大的问题是白道和月球的运动是固定的,这个方法只对少部分恒星适用。通过这个方法测出来角直径的恒星也在100颗左右。
食双星#
对于食双星,我们知道掩食时间与视向速度,那就知道线直径了。不过密近双星经常会偏离球形,同时物质交换会使得两颗恒星的光谱趋同,加大掩食时间与视向速度的测量难度。远距离双星的难度主要在于视向速度的测量方面。
热流量法#
对$$ (14.2) $$稍作变形:
$$ \frac{R}{d} = \theta_\mathrm{R} = \sqrt{\frac{\int_0^\infty F_\nu d\nu}{\sigma T_\mathrm{eff}^4}} \tag{14.4} $$
不过同样需要知道距离、有效温度以及恒星的热辐射。
热辐射可以通过恒星的光谱来估计,或者与太阳的数据作差转换成热星等,利用第十章的热改正来得到恒星的热星等。有效温度大致是从恒星模型来,也就是之后说的一些方法,直接或间接地得到。
测光半径#
热流量法要求我们知道整个光谱范围的流量,而测光半径法则走向了另一个极端。从$$ (14.1) $$我们可得:
$$ \theta_\mathrm{R} = R/d = (F_\nu/\mathscr{F}_\nu)^{1/2} \tag{14.7} $$
那如果我们能够准确知道某一个波长下的$$ F_\nu, \mathscr{F}\nu
这个方法依赖绝对定标,对测光以及模型的流量绝对定标要求不低。还有一个红外流量法,介于这两个方法之间:假设一个$$ T_\mathrm{eff}
间接方法#
表面亮度法#
还是从热流量法出发,将$$ (14.4) $$取对数并将流量转成星等,有
$$ \lg{\theta_\mathrm{R}} = - 0.2 (m_\mathrm{V} - BC) - 2\lg{T_\mathrm{eff}} + \text{constant} \tag{14.5} $$
于太阳的参数作差,把不好测量的项移到一边并定义一个新变量:
$$ \mathbb{P}\mathrm{V} = \lg{\frac{T\mathrm{eff}}{T_\mathrm{eff}^\odot}} - 0.1 (BC-BC^\odot) = -0.1 (m_\mathrm{V}-m_\mathrm{V}^\odot) - 0.5 \lg{\frac{\theta_\mathrm{R}}{\theta_\mathrm{R}^\odot}} \tag{14.10} $$
当我们有一批通过直接方法测出来的$$ \theta_\mathrm{R}
把这些结果 放到一张 图上#
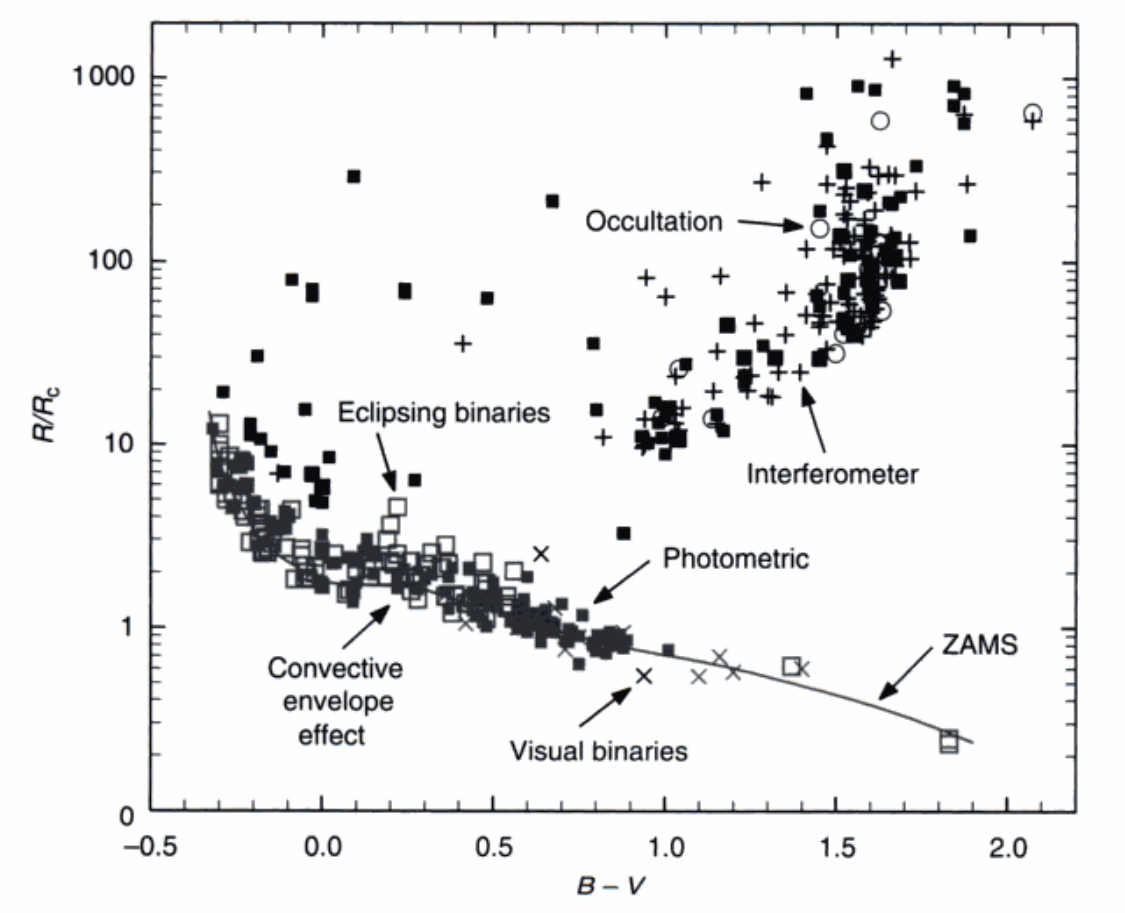
我们能从这张图上看出不少信息。
首先不同方法测出来的结果是一致的,没有哪种结果有很大偏离。对于矮星来说半径的弥散比较小,而且有一个下限零龄主序(ZAMS)在。$$ B-V > 0.5 $$的恒星演化时标比较长,所以没怎么演化,都堆在了一起;反之高温恒星的弥散就大一点了。在0.4到0.6左右矮星半径有一个快速的下降,这是因为对流传能开始占据一定比例,帮助恒星更快地收缩(但是为什么之后又慢了?)。
对巨星的分布书中没有详细的描述。
有效温度测量#
仍然从$$ (14.2) $$出发:
$$ T_\mathrm{eff} = \frac{\left( \int_0^\infty F_\nu d\nu / \sigma \right)^{1/4}}{(R/d)^{1/2}} \tag{14.14} $$
$$ T_\mathrm{eff} = \frac{T_\mathrm{eff}^\odot \left( \int_0^\infty F_\nu d\nu / \int_0^\infty F_\nu^\odot d\nu \right)^{1/4}}{(\theta_\mathrm{R}/\theta_\mathrm{R}^\odot)^{1/2}} \tag{14.15} $$
前者需要流量的绝对定标、后者和太阳作比;现在的话这俩都可以用。只不过恒星的热辐射不能完全被测出来,里面就涉及到恒星模型的帮助;那么用恒型模型也可以测出有效温度。
光球层模型法#
也就是算出一个模型来(温度分布),然后加上各个波段上的吸收系数就有辐射了。当然它的好坏取决于模型有多合适。
有效温度关系校准#
有效温度和很多的参数有关系,比如色指数和光谱型。当然误差会来自色指数的测量、星周包层带来的红化等等。既然说到了校准,我们之后就介绍一些校准有效温度的方法。毕竟多数时候有效温度只是区分恒星的一个数字,所以拿什么来校准问题都不大。
帕邢连续谱#
实际上指的是帕邢连续谱的斜率。连续谱受谱线以及$$ \log{g} $$的影响不大,基本上是LTE,还对有效温度比较敏感。当然对于高温和低温恒星不一定有用,因为它们的主要辐射不在可见光了。还有一点就是连续谱形成于比较深的地方,所以从斜率转化到有效温度的时候要注意匹配。
模型色指数#
当合成光谱质量很高的时候,我们可以去计算模型的色指数。这包括连续谱和谱线的计算,以及模型与观测星等的零点校正,还有观测波段的透过率。
巴尔末跳跃#
用于高温恒星,类似于帕邢连续谱,但是是测量巴尔末线系限左右的流量差。不过也受$$ \log{g} $$和元素丰度影响,需要进行改正。同时在线系限附近有很多的巴尔末线,连续谱不好确定。帕邢和巴尔末附近的恒星模型有的时候也给出不同的结果。
氢线#
氢线的强度对有效温度很敏感。但是氢线太胖了不好测量,以及高温之后它也会和$$ \log{g} $$有关系。
原子谱线的LDR#
这就是我的硕士毕业论文,不多说了。