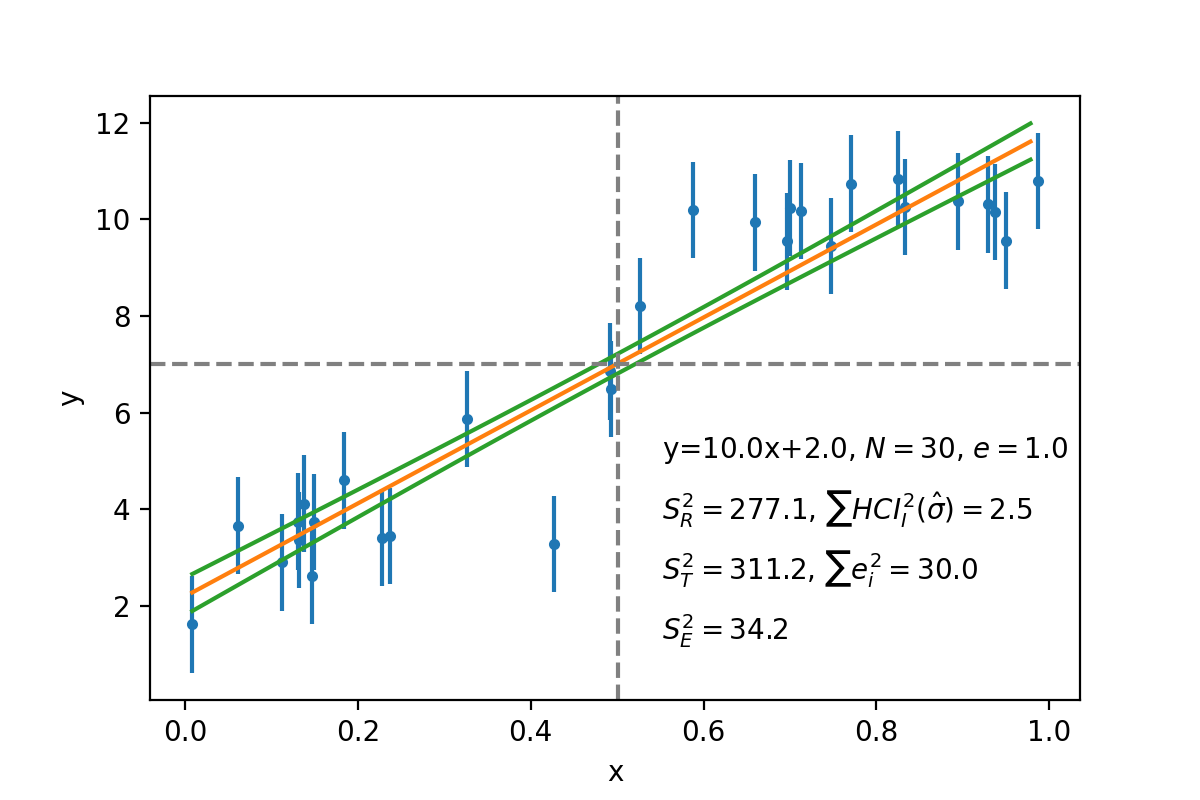
Residual in fitting#
Question#
我们想用\(y = a x + b\)拟合一个如下的线性关系:
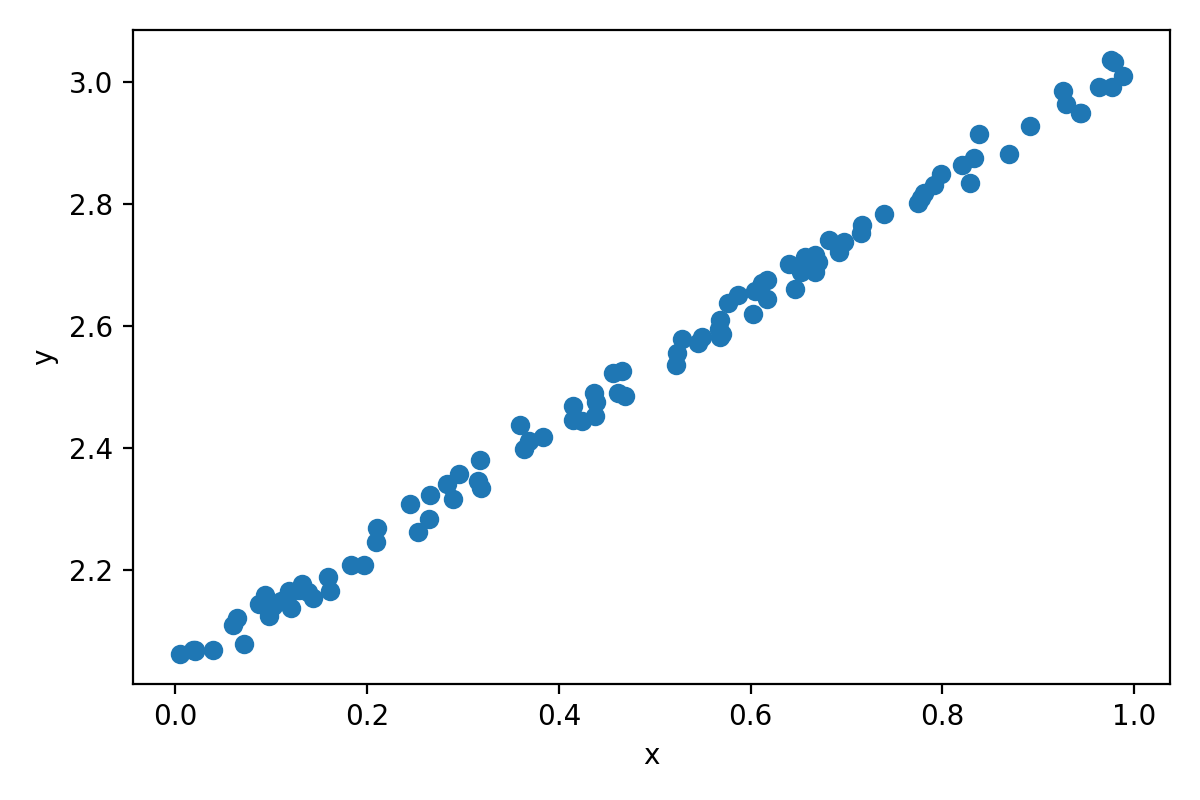
这是个Mock data,所以答案已知:
\(a = 1, b = 2\)
另有统一的观测\(y\)方向的观测误差\(e = 0.05\)以及这个线性关系的内禀弥散\(\sigma_\mathrm{r} = 0.03\),它们服从独立的高斯分布,有前述相应的\(\sigma\)
观测误差是已知的,这个关系的总弥散也可以测出来,如何通过这两个值去估计内禀弥散?
倒过来想#
我们换一个思路。因为是Mock data,我们知道观测误差、内禀弥散、总弥散以及fit出来的一切数据;这些数据怎么组合可以得到0?
从高斯分布开始#
再简化一下。我们有一组服从高斯分布的数\({y_1, y_2, ..., y_N}\),宽度(相当于观测误差,所以这里也用\(e\)表示)是我们指定的;那么总弥散和宽度有什么关系?
首先我们可以比较样本标准差(\(\mathrm{std}\))和给定的宽度(\(e\)):
$$ \mathrm{std} = \sqrt{\frac{\sum y^2}{N}} \tag{1}$$
任取一个\(N\),计算很多个\(\mathrm{std}\)、取平均值并除以\(e\),这个比值与\(N\)有如下关系(蓝点):
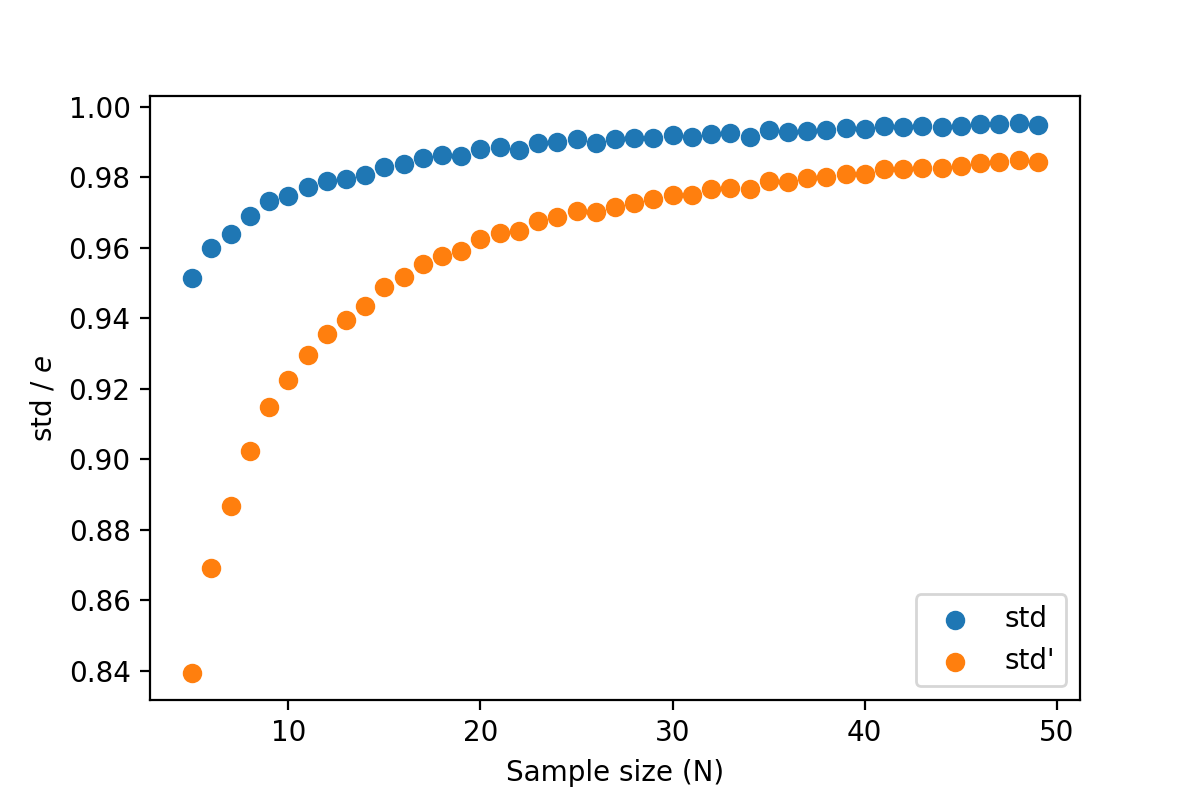
它们并不相等;实际上这是正常的,因为当\(N\)很小的时候用\(\mathrm{std}\)去估计\(e\)是不正确的;我的理解是因为样本太少而且符合高斯分布,所以取到的样本会倾向于在0左右,所以算出来的标准差偏小。这个曲线就是无偏标准差的改正曲线(维基百科)。
这个时候我们假设已知这个样本的平均值为0;\(y^2\)也就是\((y-0)^2\)。如果我们不知道真实的均值,那么就需要用样本的均值去估计,也就是把\(0\)换成\(\bar{y}\)。这个时候如果我们直接抄式子\(1\),那么画出来的比值就是上图的橙色点,是不对的。我们需要把\(N\)换成\(N-1\),也就是
$$ \mathrm{std} = \sqrt{\frac{\sum (y-\bar{y})^2}{N-1}} \tag{2}$$
这个时候两组点就很接近了(虽然我不知道为什么还有一点区别):
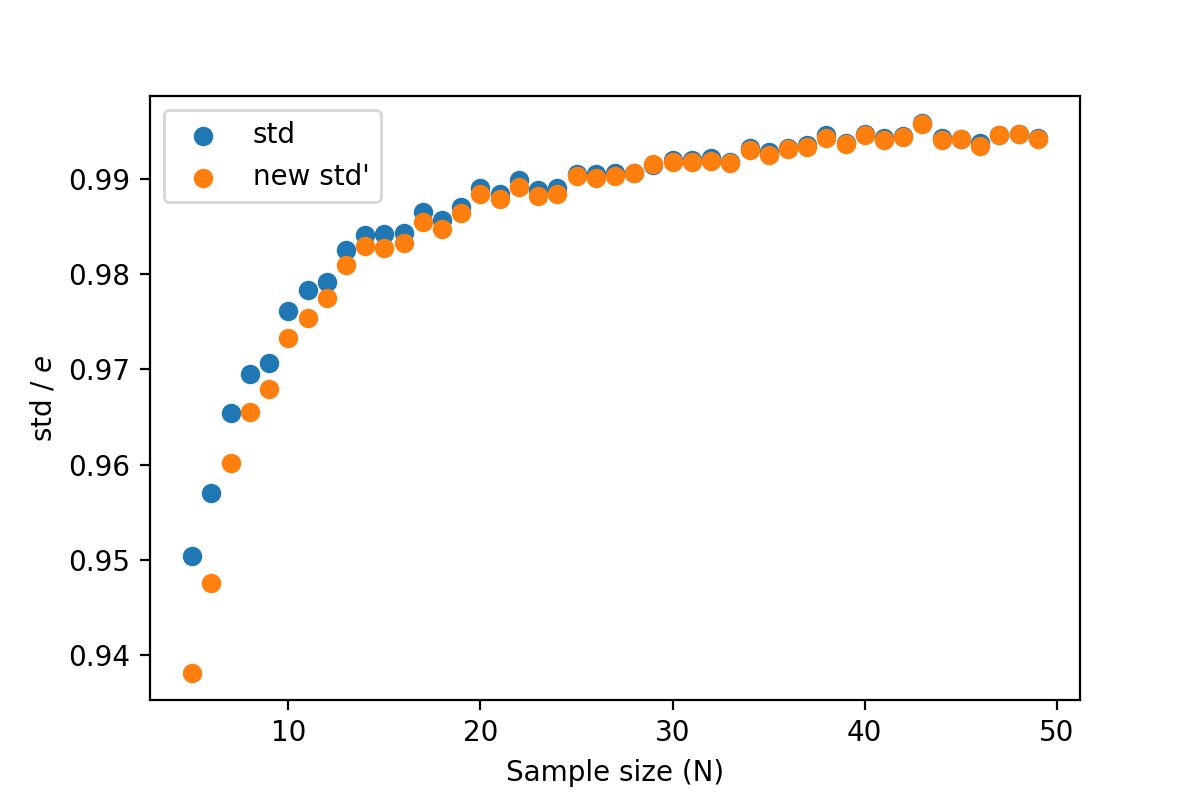
这就是贝塞尔改正。
如果是标准差呢?#
我们现在比较标准差
$$ \mathrm{res} = \sum (y-\bar{y})^2 $$
和高斯分布的宽度 \(Ne^2\) 这两者的差异。为了接近实用目的这里比较两者的差值而不是商。
当\(e = 0.5\)时,\(\mathrm{res} - Ne^2\)的值随\(N\)的变化如下:
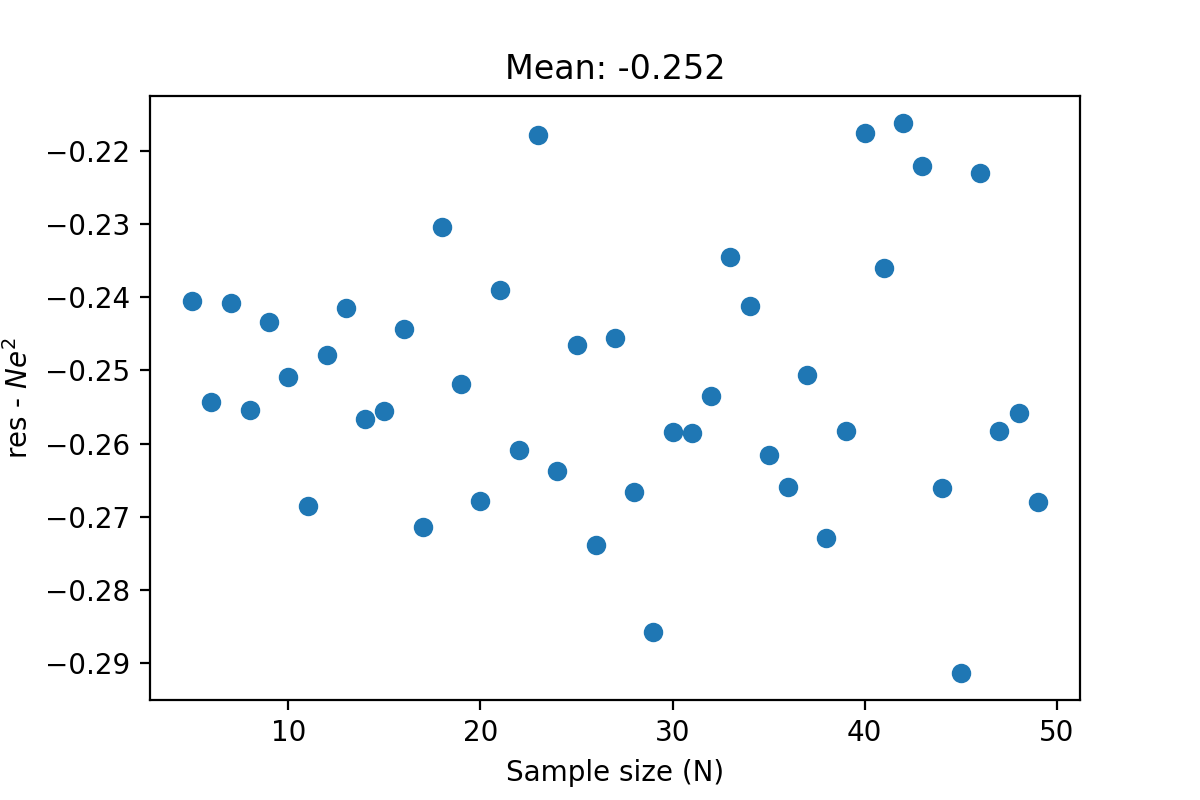
显然这不为0. 这个差值和\(e\)有关,是这样的:
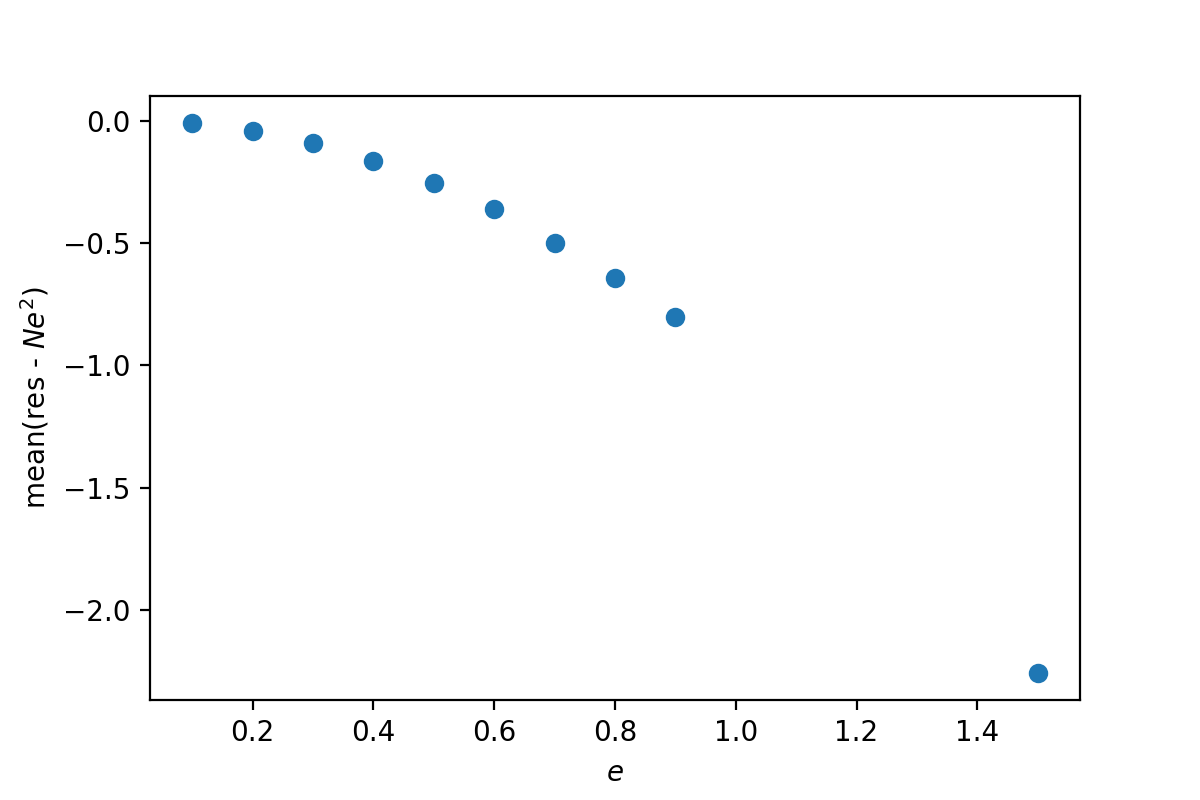
而当我们使用了改正过的\(\mathrm{res}\),\(\mathrm{res} = \sum (y-\bar{y})^2 \frac{N}{N-1}\),的时候,这个差值就不见了:
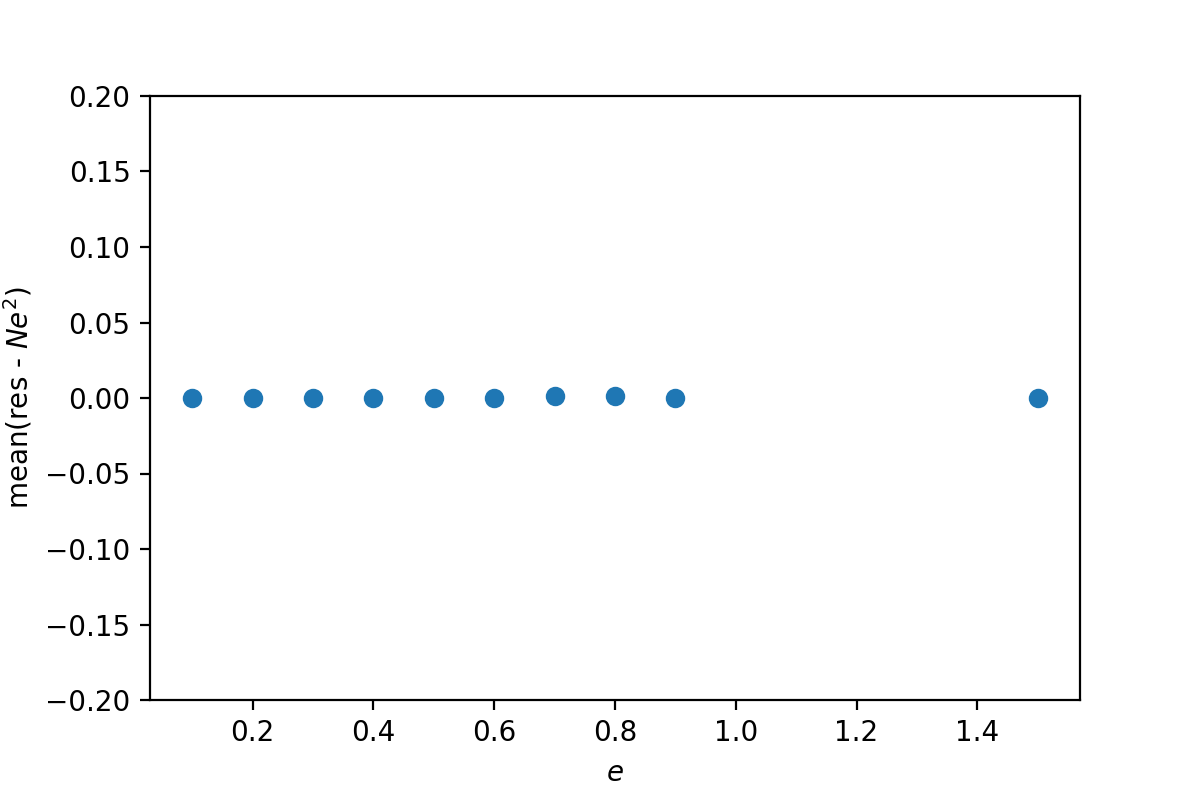
这里能得出的结论是,当\(\bar{y}\)不是一个确定值而是一个通过某种方法估计的值的时候,我们需要做一些改正,而这个改正与有多少个变量参与到了\(\bar{y}\)的计算里有关;平均值的话是1.
回到之前的问题#
现在的\(\bar{y}\)是\(y_\mathrm{cal} = ax + b\),所以\(\mathrm{res}\)应为
用这个去和\(Ne^2\)比较,就一致了。
置信区间#
尤其的是如果不做\(\frac{N}{N-2}\)而是用最初的\(\mathrm{res}\)加上每个点的\(1\sigma\)置信区间,这个量也和\(Ne^2\)是一致的。暂时不清楚原因。
\(e\)不同的话?#
看这里。 现在应该用的公式是:
$$ s^2 = \frac{\sum w_i (y-y_\mathrm{cal})^2}{V_1 - V_2/V_1} $$
$$ V_1 = \sum w_i, V_2 = \sum w_i^2 $$
用原来的公式在误差scatter为10%时开始偏离。
陈黎老师的解释#
前提:
线性关系\(y = ax + b + N(0, e)\)
每个数据点的测量误差都是\(e\)
没有额外的弥散\(\sigma_\mathrm{r}\)
\(\bar{y} = \sum{y_i} / N\)
\(\hat{y} = ax_i + b\)
$$ \hat{\sigma}^2 = \sqrt{\frac{\sum_{i=1}^N (y_i - \hat{y_i}^2)}{N-2}} $$
根据回归分析有总变差平方和等于残差平方和加上回归平方和,\(S_T^2 = S_E^2 + S_R^2\),以及
$$ \begin{align} S_T^2 &= \sum_{i=1}^N (y_i - \bar{y_i})^2 \ S_E^2 &= \sum_{i=1}^N (y_i - \hat{y_i})^2 = (N-2) \hat{\sigma}^2 \ S_R^2 &= \sum_{i=1}^N (\hat{y_i} - \bar{y_i})^2 \end{align}$$
实际上\(\sum_{i=1}^N HCI_i^2(\hat{\sigma}) \approx S_R^2\)以及\(\sum_{i=1}^N e_i^2 = S_T^2\)。