第三章：光谱仪#
我们需要光谱仪，没有光谱仪哪来的光谱。低分辨率光谱仪可以得到天体的连续谱（第十章），而高分辨率的光谱仪可以得到天体的谱线（第十二章）。
概述#
光谱仪示意图
从望远镜中过来的光在狭缝的中心聚焦，然后被准直器变为平行光照到光栅上面，色散后经过改正镜再被聚焦到CCD上。单色光会在焦面上形成一条线；而因为一般狭缝的宽度都比较大，最终在焦面形成的线宽基本不受光栅衍射条纹的影响。而当复色光入射到光谱仪的时候，焦面上将形成一段连续谱。连续谱中每个颜色的“纯净”程度由\(\Delta \lambda\)决定。\(\Delta \lambda\)越小，色散程度越大，天文学家们越高兴。不过色散程度也需要和天体入射的光的总量协调，因为色散程度越大每个像素的光流量越小，需要的积分时间就越长。一般来说我们需要\(\Delta \lambda\)小于我们关心的光谱结构；第十二章有定量计算。
衍射光栅及其原理#
衍射光栅示意图
令\(P(0)\)所指示的点为相位0点，则在光栅上任一点和它的相位差为\(x \sin{\alpha}\)；\(\alpha\)为入射平面光法向与光栅法向的夹角，是一个定值。所以我们可以将在光栅上的入射光表达为：
$$ F(x, t) = F_0(t)e^{2\pi i\frac{x\sin{\alpha}}{\lambda}} \tag{3.1}$$
同时因为入射光的频率很大，积分时间一般又比较长，所以可以将\(F_0(t)\)用它的平均值\(F_0\)代替。
令\(G(x)\)为光栅，
$$ G(x) = \begin{cases} 1 & \mathrm{狭缝中}\ 0 & \mathrm{狭缝外} \end{cases}$$
在\(\beta\)角上看到的光强为\(F(x, t)\)与\(G(x)\)的乘积加上离开光栅后的相位差在\(x\)上的积分：
$$ \begin{align} g(\beta) & = \int^{\infty}{-\infty} F(x, t) e^{2\pi i\frac{x\sin{\beta}}{\lambda}} G(x) dx \ & = F_0\int^{\infty}{-\infty} G(x) e^{2\pi i\frac{x\sin{\alpha}+x\sin{\beta}}{\lambda}} dx \end{align}$$
令\(\theta = \frac{\theta'}{\lambda} = \frac{\sin{\alpha} + \sin{\beta}}{\lambda}\)，有
$$ g(\theta) = F_0 \int^{\infty}_{-\infty} G(x) e^{2\pi ix\theta} dx \tag{3.2}$$
将这个式子与第二章的傅里叶变换定义式比较，我们发现它们是一样的，所以光栅就相当于一个傅里叶变换器。因为这里\(F_0\)是一个常数，重要的是后面的积分，所以之后我们将直接讨论\(G(x)\)的傅里叶变换。
\(G(x)\)的傅里叶变换#
\(G(x)\)是由宽为\(b\)的狭缝等距\(d\)摆放直至充满宽度\(W\)而来的：
$$ G(x) = B_1(x) * III(x) B_2(x) \tag{3.3}$$
\(B_1(x)\)为单个狭缝，它与\(III(x)\)的卷积为无限宽的光栅，\(B_2(x)\)为光栅的宽度。它的傅里叶变换为：
$$ \begin{align} g(\theta) &= b_1(\theta) iii(\theta) * b_2(\theta) \ & = \frac{b\sin{\pi\theta b}}{\pi\theta b} iii(\theta) * \frac{W\sin{\pi\theta W}}{\pi\theta W} \end{align}$$
将Shah函数用\(\delta\)函数表达：
$$ \begin{align} g(\theta) & = \sum \delta(\theta-\frac{n}{d}) * \frac{W\sin{\pi\theta W}}{\pi\theta W} \frac{b\sin{\pi\theta b}}{\pi\theta b} \ & = \sum_n \frac{W\sin{\pi(\theta-\frac{n}{d}) W}}{\pi(\theta-\frac{n}{d}) W} \frac{b\sin{\pi\theta b}}{\pi\theta b} \end{align} \tag{3.4}$$
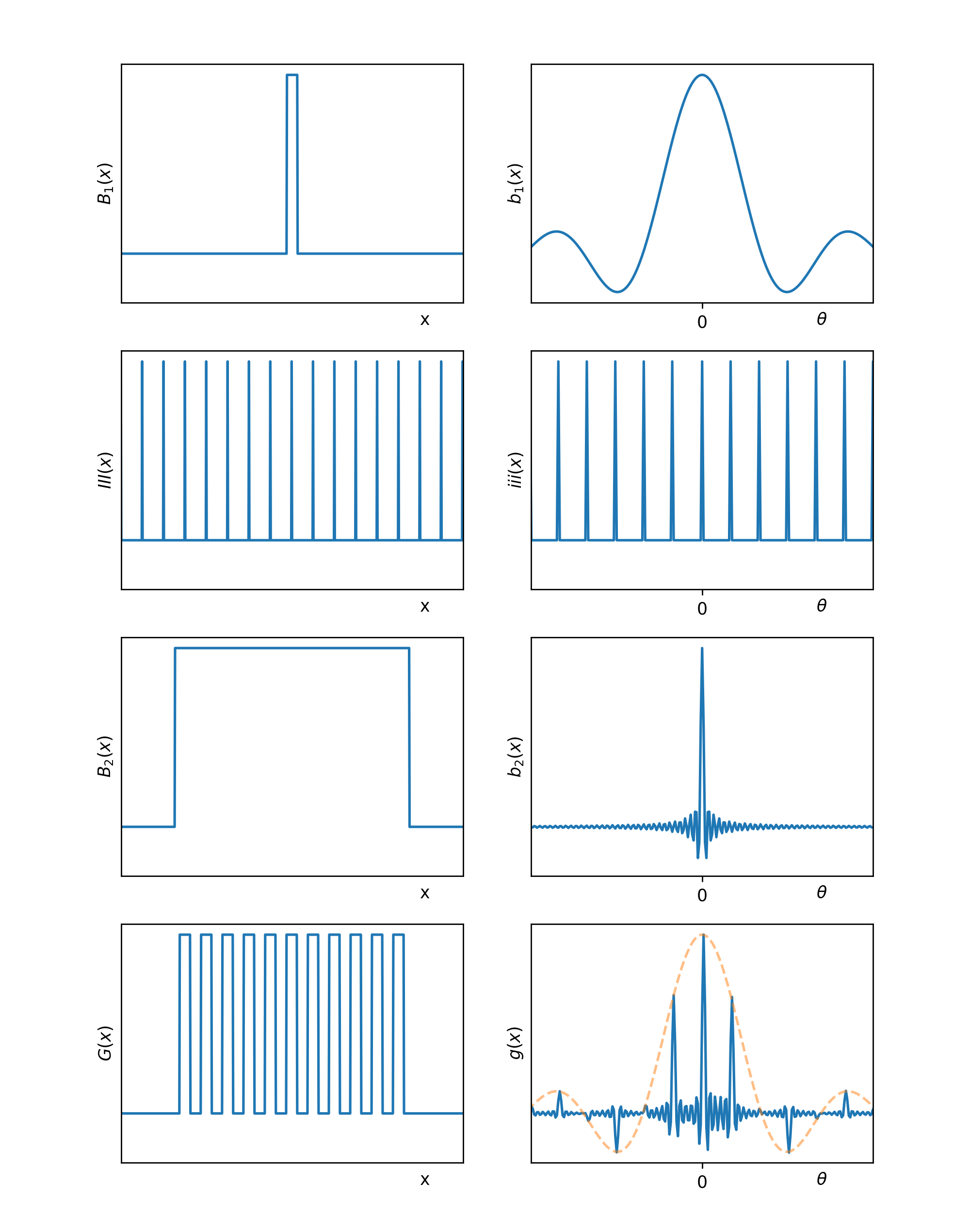光栅以及它的傅里叶变换
在小角度下\(d\theta'\)和\(d\beta\)近似是一样的：
$$ \sin{\alpha} + \sin{\beta} = \theta’ \Rightarrow d\theta’ = \cos{\beta} d\beta \approx d\beta $$
每个尖峰下降到0时的宽度由\(B_2(x)\)决定：
$$ \Delta \theta’ = \frac{\lambda}{W} $$
每个尖峰的位置由\(III(x)\)决定：
$$ \theta’ = \frac{n\lambda}{d} = \sin{\alpha} + \sin{\beta} \tag{3.5}$$
所以不同波长的光有不同的宽度和尖峰位置。这里的\(n\)称为级数，0级光谱所有波长的光都集中在\(x=0\)处，所以为白光。1级和其他级光谱的分辨率为：
$$ \frac{d\theta’}{d\lambda} = \frac{n}{d} \tag{3.6}$$
将\(\Delta \theta' = \frac{\lambda}{W}\)代入\((3.6)\)，得：
$$ \Delta \lambda = \frac{\lambda}{W} \frac{d}{n} \tag{3.7}$$
这个量可以理解为单位角度上的波长改变量是多少；我们当然希望它越小越好，所以\(n\)小的时候要增大板宽和多刻线；\(n\)大的时候则不一定。
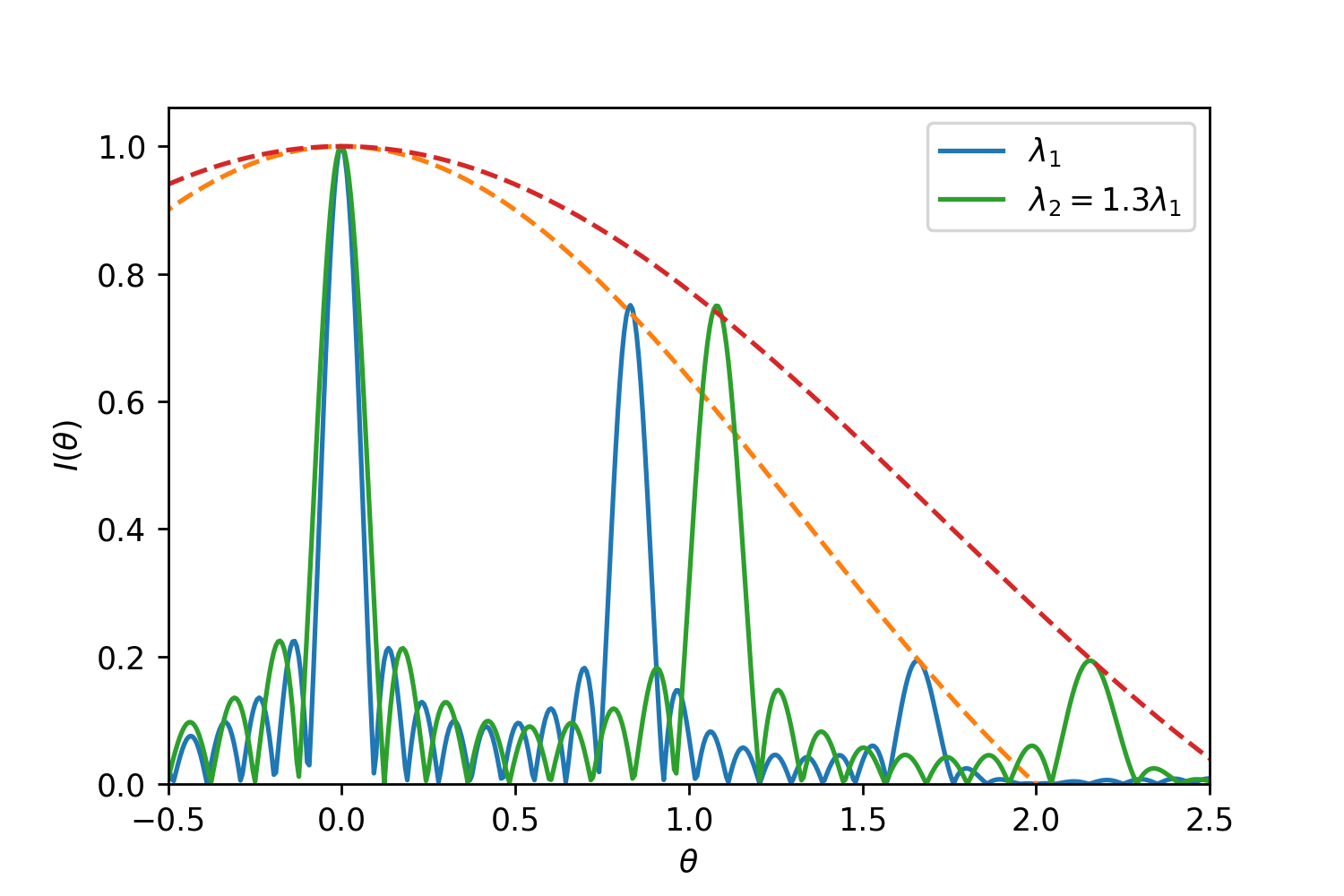复色光入射时的情况
闪耀光栅#
上图中我们可以看到透射光栅的光谱受到狭缝宽度影响，主要的能量落在了0级处，并没有分开。我们自然不希望这样，而是想让多数的光落在我们想要的级数上。要做到这一点，我们只需要将\(b_2(\theta)\)的最高点从0移动到对应的级数位置即可。第二章傅里叶变换的性质2表明如果想在某个域上平移函数，需要在另一个域上引入相位差，在这里也就是不同的光程。实际的操作可以在狭缝中插入三棱镜让光线偏转，但是棱镜会带来色散，而且这样的光栅也很难制作。所以常用的是将狭缝改成倾斜的面镜，从而将光反射到某个特定角度。这样的光栅叫闪耀光栅，光栅法线与槽面法线之间的夹角\(\phi\)叫闪耀角(在法线同侧的角度正负号相同)。
闪耀光栅（右）示意图
这个时候式子\((3.4)\)的最后一项发生了变化，\(\alpha, \beta\)变成了\(\alpha-\phi, \beta-\phi\)。这里用减号的原因是虽然对于槽面来说，图示的\(\phi\)角会使得入射角和反射角都增大，但是\((3.4)\)中的\(\alpha, \beta\)指的是箭头所指的线段长度，这两段线在反射光栅的情况下都减小了。所以对于归一化的这一项，我们有：
$$ I(\beta) = \left[\frac{\sin{\left{ \pi b/\lambda [\sin{(\alpha-\phi)}+\sin{(\beta-\phi)}]\right}}}{\pi b/\lambda [\sin{(\alpha-\phi)}+\sin{(\beta-\phi)}]}\right]^2 \tag{3.8}$$
因为光栅的分光，只有符合\((3.5)\)的波长的光才能通过，所以我们可以将\((3.5)\)代入\((3.8)\)消去\(\lambda\)（注意\((3.5)\)中的\(\alpha, \beta\)不变），得到：
$$ I(\beta) = \left[\frac{\sin{\left{ n\pi b/d [\cos{\phi}-\sin{\phi}\frac{\cos{\alpha}+\cos{\beta}}{\sin{\alpha}+\sin{\beta}}]\right}}}{n\pi b/d [\cos{\phi}-\sin{\phi}\frac{\cos{\alpha}+\cos{\beta}}{\sin{\alpha}+\sin{\beta}}]}\right]^2 \tag{3.8}$$
示例图如下：
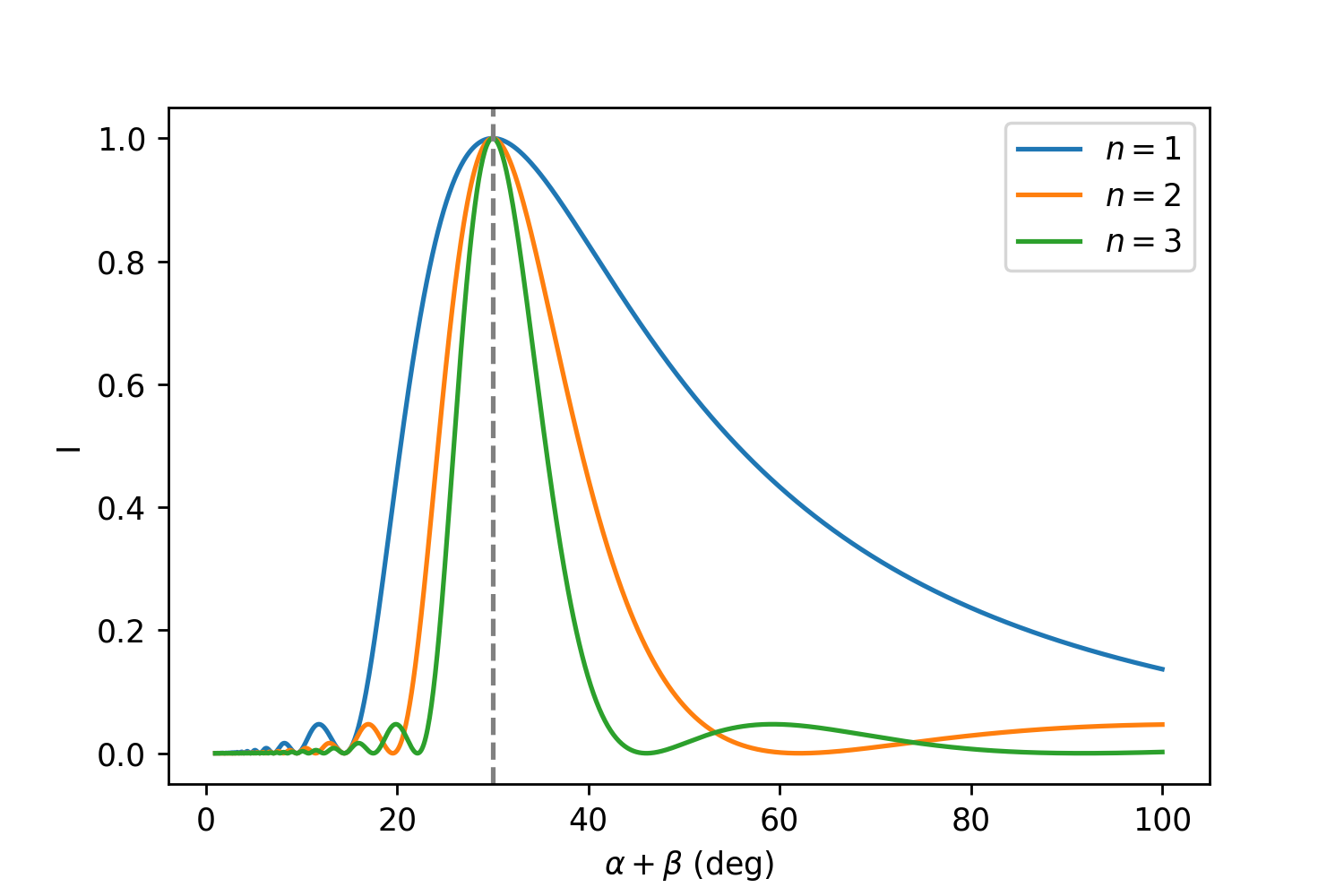闪耀光栅的光强包络线，\(\phi=15^\circ \)$
可以看到这个时候整个函数的最大值被推到了\(\alpha+\beta = 2\phi\)的地方。当然我们也可以用\(\lambda\)作为自变量，画出\(I(\beta)\)随\(\lambda\)的变化情况。
利特罗条件#
一般来说光栅在制造的时候会被造成当入射角和衍射角一样的时候，1级光谱会被闪耀，这被叫做利特罗条件。但是当入射光线和衍射光线在同一个方向的时候，我们并不能接收到光谱，所以一般使用的是别的入射角；这种情况下1级光谱的闪耀波长会发生变化。假设利特罗条件下的闪耀波长为\(\lambda_0\)，则根据\((3.5)\)有：
$$ \frac{n\lambda}{d} = \sin{\alpha} + \sin{\beta} $$
$$ \begin{align} \frac{n\lambda_0}{d} &= 2\sin{\phi} \ &= 2\sin{\alpha+\beta} \end{align} $$
两式相除，得：
$$ \lambda = \lambda_0 \cos{0.5(\alpha-\beta)} $$
阴影#
光栅的摆放方式有很多种。我们之前讨论的都是入射光线和光栅法线在槽面法线的两侧；当然也可以倒过来摆，将入射光线和光栅法线放在槽面法线的同一侧(\(\alpha < \beta\)的时候)。不过这样的话会引起一部分的光在反射后照射到槽的侧面，引起光损和杂散光。光损比例由下式决定：
$$ f=\frac{2\tan{\phi}\tan{\beta-\phi}}{1+\tan{\phi}\tan{\beta-\phi}} $$
如果光谱仪有缺陷#
首先有周期性缺陷的光谱仪一般会产生鬼线。这样的光谱仪相当于两个光谱仪的叠加：
$$ G’(x) = G(x)H(x) $$
$$ H(x) = B_3(x) * III(x) B_2(x) $$
所以“缺陷光谱仪”会在原来的谱线周围再加上一堆鬼线。如果周期性缺陷相对于原来的光谱的间隔很大，那么鬼线会在母线（原来的谱线）附近。我们可以仿照\((3.5)\)并且代入\((3.6)\)写出鬼线的\(\Delta \lambda\)：
$$ \Delta \theta_g = \frac{m\lambda_g}{D} $$
$$ \Delta \lambda_g = \frac{d}{n}\frac{m}{D}\lambda_g $$
所以鬼线是等距分布的。鬼线的光强比较复杂，但是一般母线的强度最大。
还有另外的几种因缺陷引起的线，如卫星线（有一块刻歪了）等。
色散和分辨率#
分辨率是光谱仪很重要的一个参数。但是在讨论分辨率之前我们需要分清楚它和色散的区别。
角、线色散#
如上图，如果两束不同波长的光射入镜头的角度为\(\Delta \beta\)，则称它们的角色散为\(\Delta \beta\)。角色散的大小是由光栅决定的，具体来说是\((3.6)\)式。这个角度最终在焦平面上投影的长度叫做线色散，易得：
$$ \Delta x = f_\mathrm{cam} \Delta \beta $$
或者
$$ \frac{d\beta}{dx} = \frac{1}{f_\mathrm{cam}} $$
将角度转化成波长，有：
$$ \begin{align} \frac{d\lambda}{dx} &= \frac{d\lambda}{d\beta} \frac{d\beta}{dx} \ &= \frac{1}{f_\mathrm{cam}} \frac{1}{d\beta/d\lambda} \ &= \frac{1}{f_\mathrm{cam}} \frac{d\cos{\beta}}{n} \tag{3.13} \end{align} $$
这里没有小角度入射的假设，所以有一个\(\cos{\beta}\)在。同样，高的色散程度对应着小的\(\frac{d\lambda}{dx}\)。
分辨率#
我们从狭缝的大小开始考虑。令\(f_\mathrm{coll}, f_\mathrm{cam}\)为准直器、成像相机的焦距，在小角度情况下，宽度为\(W'\)的狭缝在准直器（或者光栅）上的角度为：
$$ \Delta \alpha = \frac{W’}{f_\mathrm{coll}} $$
对\((3.5)\)式求导，得出：
$$ \Delta\beta = -\frac{\cos{\alpha}}{\cos{\beta}} \Delta \alpha $$
所以
$$ \Delta \beta = -\frac{\cos{\alpha}W’}{\cos{\beta}f_\mathrm{coll}} $$
令\(w\)为狭缝在CCD上的像宽，则
$$ \begin{align} w &= \Delta \beta f_\mathrm{cam} \ &= -\frac{\cos{\alpha}}{\cos{\beta}} \frac{f_\mathrm{cam}}{f_\mathrm{coll}} W’ \tag{3.14} \end{align}$$
\({w/W'}\)正比于\(f_\mathrm{cam}/f_\mathrm{coll}\)。一般来说我们需要CCD的像素与狭缝在CCD上的像宽相匹配，最好是1个单位像宽对应CCD上的两个像素（奈奎斯特频率）。稍微的过采样可能会有好处，但是面临着更长时间曝光和深度减小的问题；而欠采样会使得信息丢失。
我们也可以将像宽\(w\)转换成单位长度上的波长改变量（分辨率）：
$$ \begin{align} \Delta \lambda &= w \frac{d\lambda}{dx} \ &= -\frac{\cos{\alpha}}{\cos{\beta}} \frac{f_\mathrm{cam}}{f_\mathrm{coll}} W’ \frac{1}{f_\mathrm{cam}} \frac{d\cos{\beta}}{n} \ &= -\cos{\alpha} \frac{W’d}{f_\mathrm{coll}n} \tag{3.15}\end{align} $$
可以看出分辨率与成像相机的焦距没有关系。提升分辨率可以通过改变上式的参数，但是一般会导致光损(减小\(W'\))或者需要更大/更好的光栅(增大\(f_\mathrm{coll}\)或者\(n\))。
阶梯光谱仪#
通过增大\(n\)来提高分辨率实际上没那么简单。使用高级数光谱的时候，虽然光谱的确被色散到了更宽的角度上（当然传统上这意味着需要更长的CCD），但是不同级数的光谱会发生重叠，使得不同（但是分立）波长的光同时照到了一个像素上。
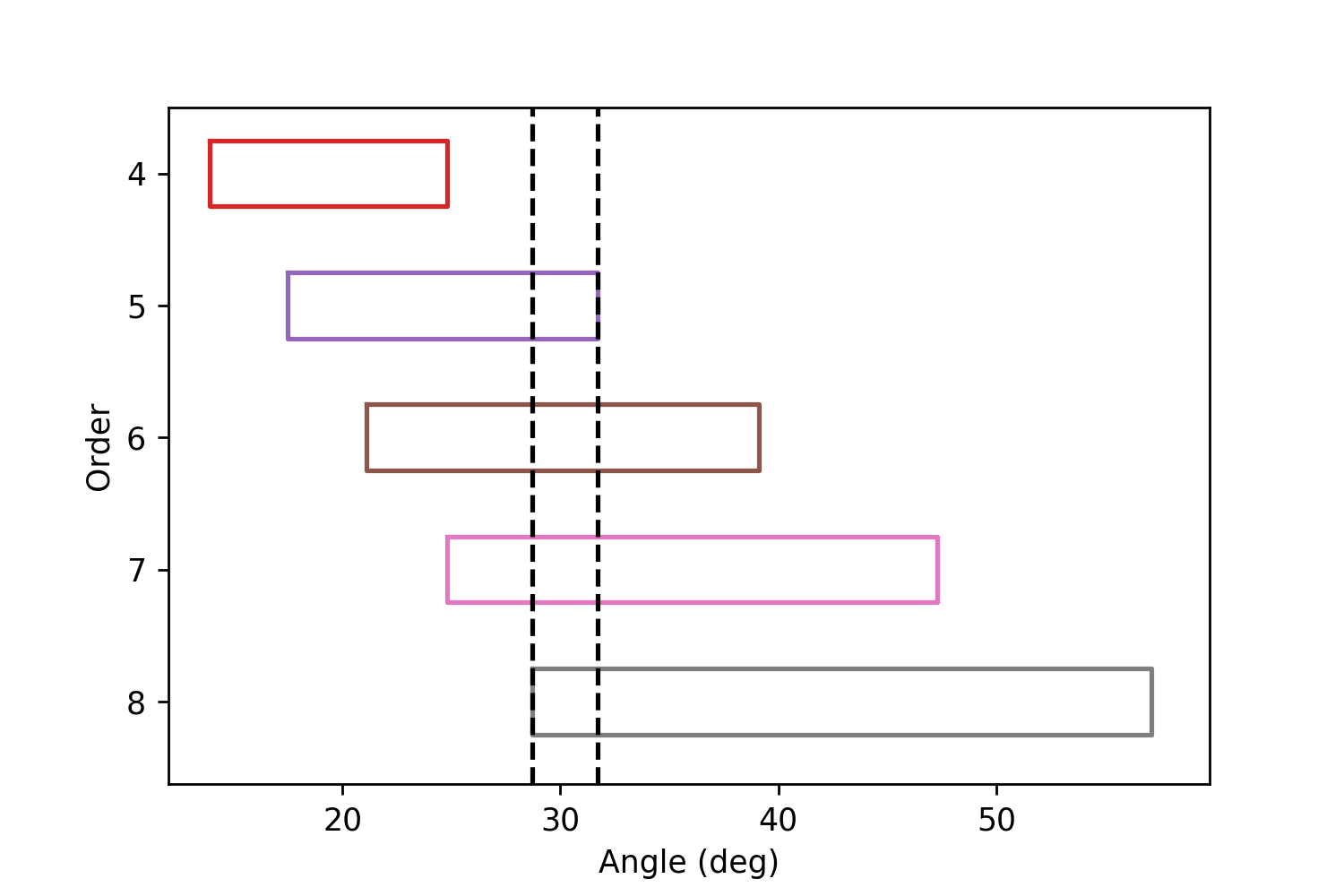高级数光谱重叠情况；选择的当的话黑色虚线中间可以包含了整个波长范围的光
那么如果我们截取某一段区域，使得这段区域几个级数的光谱加起来刚好覆盖我们想要的波长，然后在后面加上一个在另一个方向上色散的光栅，就可以把光谱分成独立的条状并且覆盖很宽的波长范围；这就是阶梯光谱仪。
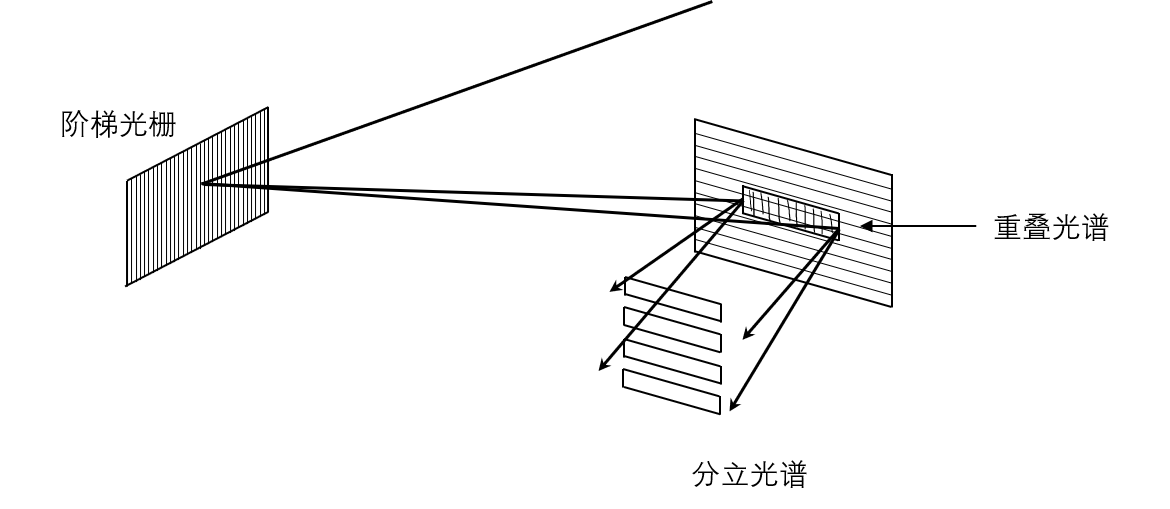阶梯光谱仪示意图
阶梯光谱仪的一个例子是京都产业大学制造的WINERED：
图中下方从右到左为狭缝、准直镜以及阶梯光栅，中间的白色部分为CCD。这个光谱仪波长虽然在近红外(
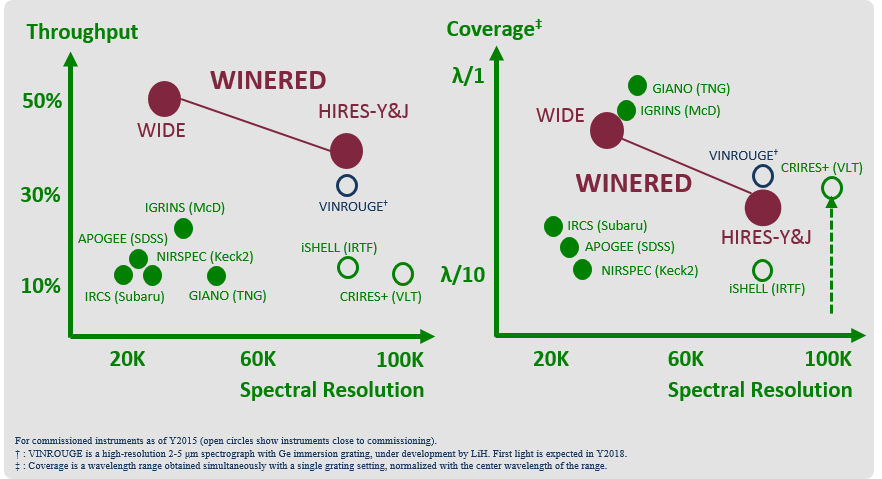WINERED与其他光谱仪参数对比
略过的内容#
多目标光谱仪、迈克尔逊干涉仪、望远镜基础